Ley de Senos y Cosenos
Ley del seno y coseno
El triángulo ABC es un triángulo rectángulo y lo usaremos para definir las funciones seno y coseno.
En un triángulo rectángulo, el seno (abreviado como sen o sin) es la razón entre el cateto opuesto y la hipotenusa.
sen α = cos β = |BC| / |AB| = |BC| / 1 = |BC| = a
Para cualquier triangulo se verifica el Teorema del seno que demuestra que: «Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos»:
El coseno (abreviado como cos) es la razón entre el cateto adyacente y la hipotenusa.
Si usamos una circunferencia unitaria (con radio igual a uno), entonces la hipotenusa, AB, del triángulo se hace 1, por lo que las relaciones quedan
cos α = sen β = |AC| / |AB| = |AC| / 1 = |AC| = b
Para cualquier triangulo se verifica el Teorema del coseno que demuestra que: «El cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido»:
a2 = b2 + c2 − 2bc * cos(A)
b2 = a2 + c2 − 2ac * cos(B)
c2 = a2 + b2 − 2ab * cos(C)
Medidas de tendencia y disperción
Las medidas de tendencia central son medidas estadísticas que pretenden resumir en un solo valor a un conjunto de valores. Representan un centro en torno al cual se encuentra ubicado el conjunto de los datos. Las medidas de tendencia central más utilizadas son: media, mediana y moda. Las medidas de dispersión en cambio miden el grado de dispersión de los valores de la variable. Dicho en otros términos las medidas de dispersión pretenden evaluar en qué medida los datos difieren entre sí. De esta forma, ambos tipos de medidas usadas en conjunto permiten describir un conjunto de datos entregando información acerca de su posición y su dispersión.
Los procedimientos para obtener las medidas estadísticas difieren levemente dependiendo de la forma en que se encuentren los datos. Si los datos se encuentran ordenados en una tabla estadística diremos que se encuentran “agrupados” y si los datos no están en una tabla hablaremos de datos “no agrupados”.
Según este criterio, haremos primero el estudio de las medidas estadísticas para datos no agrupados y luego para datos agrupados.
Promedio o media
La medida de tendencia central más conocida y utilizada es la media aritmética o promedio aritmético. Se representa por la letra griega µ cuando se trata del promedio del universo o población y por Ȳ (léase Y barra) cuando se trata del promedio de la muestra. Es importante destacar que µ es una cantidad fija mientras que el promedio de la muestra es variable puesto que diferentes muestras extraídas de la misma población tienden a tener diferentes medias. La media se expresa en la misma unidad que los datos originales: centímetros, horas, gramos, etc.
Si una muestra tiene cuatro observaciones: 3, 5, 2 y 2, por definición el estadígrafo será:
Estos cálculos se pueden simbolizar:
Donde Y1 es el valor de la variable en la primera observación, Y2 es el valor de la segunda observación y así sucesivamente. En general, con “n” observaciones, Yi representa el valor de la i-ésima observación. En este caso el promedio está dado por
De aquí se desprende la fórmula definitiva del promedio:
Desviaciones: Se define como la desviación de un dato a la diferencia entre el valor del dato y la media:
Mediana
Otra medida de tendencia central es la mediana. La mediana es el valor de la variable que ocupa la posición central, cuando los datos se disponen en orden de magnitud. Es decir, el 50% de las observaciones tiene valores iguales o inferiores a la mediana y el otro 50% tiene valores iguales o superiores a la mediana.
Si el número de observaciones es par, la mediana corresponde al promedio de los dos valores centrales. Por ejemplo, en la muestra 3, 9, 11, 15, la mediana es (9+11)/2=10.
Moda
La moda de una distribución se define como el valor de la variable que más se repite. En un polígono de frecuencia la moda corresponde al valor de la variable que está bajo el punto más alto del gráfico. Una muestra puede tener más de una moda.
Medidas de dispersión
Las medidas de dispersión entregan información sobre la variación de la variable. Pretenden resumir en un solo valor la dispersión que tiene un conjunto de datos. Las medidas de dispersión más utilizadas son: Rango de variación, Varianza, Desviación estándar, Coeficiente de variación.
Rango de variación
Se define como la diferencia entre el mayor valor de la variable y el menor valor de la variable.
La mejor medida de dispersión, y la más generalizada es la varianza, o su raíz cuadrada, la desviación estándar. La varianza se representa con el símbolo σ² (sigma cuadrado) para el universo o población y con el símbolo s2 (s cuadrado), cuando se trata de la muestra. La desviación estándar, que es la raíz cuadrada de la varianza, se representa por σ (sigma) cuando pertenece al universo o población y por “s”, cuando pertenece a la muestra. σ² y σ son parámetros, constantes para una población particular; s2 y s son estadígrafos, valores que cambian de muestra en muestra dentro de una misma población. La varianza se expresa en unidades de variable al cuadrado y la desviación estándar simplemente en unidades de variable.
Fórmulas
Donde µ es el promedio de la población.
Donde Ȳ es el promedio de la muestra.
Consideremos a modo de ejemplo una muestra de 4 observaciones
Según la fórmula el promedio calculado es 7, veamos ahora el cálculo de las medidas de dispersión:
s2 = 34 / 3 = 11,33 Varianza de la muestra
La desviación estándar de la muestra (s) será la raíz cuadrada de 11,33 = 3,4.
Interpretación de la varianza (válida también para la desviación estándar): un alto valor de la varianza indica que los datos están alejados del promedio. Es difícil hacer una interpretación de la varianza teniendo un solo valor de ella. La situación es más clara si se comparan las varianzas de dos muestras, por ejemplo varianza de la muestra igual 18 y varianza de la muestra b igual 25. En este caso diremos que los datos de la muestra b tienen mayor dispersión que los datos de la muestra a. esto significa que en la muestra a los datos están más cerca del promedio y en cambio en la muestra b los datos están más alejados del promedio.
Coeficiente de variación
Es una medida de la dispersión relativa de los datos. Se define como la desviación estándar de la muestra expresada como porcentaje de la media muestral.
Es de particular utilidad para comparar la dispersión entre variables con distintas unidades de medida. Esto porque el coeficiente de variación, a diferencia de la desviación estándar, es independiente de la unidad de medida de la variable de estudio.
Medidas de tendencia central y de dispersión en datos agrupados
Se identifica como datos agrupados a los datos dispuestos en una distribución de frecuencia. En tal caso las fórmulas para el cálculo de promedio, mediana, modo, varianza y desviación estándar deben incluir una leve modificación. A continuación se entregan los detalles para cada una de las medidas.
Promedio en datos agrupados
La fórmula es la siguiente:
Donde ni representa cada una de las frecuencias correspondientes a los diferentes valores de Yi.
Consideremos como ejemplo una distribución de frecuencia de madres que asisten a un programa de lactancia materna, clasificadas según el número de partos. Por tratarse de una variable en escala discreta, las clases o categorías asumen sólo ciertos valores: 1, 2, 3, 4, 5.
Entonces las 42 madres han tenido, en promedio, 2,78 partos.
Si la variable de interés es de tipo continuo será necesario determinar, para cada intervalo, un valor medio que lo represente. Este valor se llama marca de clase (Yc) y se calcula dividiendo por 2 la suma de los límites reales del intervalo de clase. De ahí en adelante se procede del mismo modo que en el ejercicio anterior, reemplazando, en la formula de promedio, Yi por Yc.
Mediana en datos agrupados
Si la variable es de tipo discreto la mediana será el valor de la variable que corresponda a la frecuencia acumulada que supere inmediatamente a n/2. En los datos de la tabla 1 Me=3, ya que 42/2 es igual a 21 y la frecuencia acumulada que supera inmediatamente a 21 es 33, que corresponde a un valor de variable (Yi) igual a 3.
Si la variable es de tipo continuo es necesario, primero, identificar la frecuencia acumulada que supere en forma inmediata a n/2, y luego aplicar la siguiente fórmula:
Donde:
Moda en datos agrupados
Si la variable es de tipo discreto la moda o modo será al valor de la variable (Yi) que tenga la mayor frecuencia absoluta ( ). En los datos de la tabla 1 el valor de la moda es 3 ya que este valor de variable corresponde a la mayor frecuencia absoluta =16.
Más adelante se presenta un ejemplo integrado para promedio, mediana, varianza y desviación estándar en datos agrupados con intervalos.
Varianza en datos agrupados
Para el cálculo de varianza en datos agrupados se utiliza la fórmula
Con los datos del ejemplo y recordando que el promedio (Y) resultó ser 2,78 partos por madre,
Cuando los datos están agrupados en intervalos de clase, se trabaja con la marca de clase (Yc), de tal modo que la fórmula queda:
Donde Yc es el punto medio del intervalo y se llama marca de clase del intervalo
Yc= (Límite inferior del intervalo + limite superior del intervalo)/2
Probabilidad Condicional
Probabilidad condicional es la probabilidad de que ocurra un evento A, sabiendo que también sucede otro evento B. La probabilidad condicional se escribeP(A|B), y se lee «la probabilidad de A dado B».
No tiene por qué haber una relación causal o temporal entre A y B. A puede preceder en el tiempo a B, sucederlo o pueden ocurrir simultáneamente. A puede causar B, viceversa o pueden no tener relación causal. Las relaciones causales o temporales son nociones que no pertenecen al ámbito de la probabilidad. Pueden desempeñar un papel o no dependiendo de la interpretación que se le dé a los eventos.
Un ejemplo clásico es el lanzamiento de una moneda para luego lanzar un dado. ¿Cuál es la probabilidad de obtener una cara (moneda) y luego un 6 (dado)? Pues eso se escribiría como P (Cara | 6).
El condicionamiento de probabilidades puede lograrse aplicando el teorema de Bayes.
Dado un espacio de probabilidad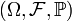 
y dos eventos (o sucesos) 
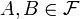con 
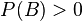, la probabilidad condicional de A dado B está definida como:
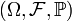y dos eventos (o sucesos) 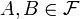con 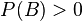, la probabilidad condicional de A dado B está definida como:
Probabilidad Clasica
PROBABILIDAD CLÁSICA
Es el número de resultados favorables a la presentación de un evento dividido entre el número total de resultados posibles. Asignación de probabilidad "a priori", si necesidad de realizar el experimento.
La probabilidad clásica o teórica se aplica cuando cada evento simple del espacio muestral tiene la misma probabilidad de ocurrir.
Fórmula para obtener la probabilidad clásica o teórica:
EJEMPLO: ¿Cuál es la probabilidad de obtener un número mayor que 3, en el lanzamiento de un dado? Si E: 4, 5, 6, entonces el número de resultados favorables es n (E) = 3.
Si S: 1, 2, 3, 4, 5, 6, entonces el número total de resultados posibles es (S) = 6.
Por lo tanto:
